The Anvikshik

Page Rank

September 24, 2020

In the last post, we saw how the concept of hubs and authorities can help in identifying the relevant pages for a query on the web or a corpus of documents. Today, we will look into an interesting algorithm called PageRank developed by Larry Page and Sergey Brin when they were studying at Stanford. The motivation behind this algorithm was to look for a way to rank the web pages which are not only hetergenous in nature but also are not controlled by any central authority.

The main idea behind this algorithm is to use the "backlinks" to increase the importance of any webpage. For e.g if an Information Retrieval course cites this blog post, then PageRank of my web page will increase. Furthermore, if the course happens to be from MIT/Stanford/Berkeley etc. then it would increase the PageRank of this blog even more i.e backlinks from important pages are signficant than backlinks from average pages. For example, in the title figure where size represents PageRank, we can see that page E has higher PageRank than page G of the same row even though it has fewer backlinks. This is because one of the links to E comes from an important page L and thus is of higher importance. 

Tutorial on how to calculate PageRank:

There are two ways to calculate the PageRank- one is using Matrices and Eigenvalues (refer IR_STANFORD for an example) and the another is using "waterflow" model. I will be using the "waterflow" model to explain how PageRank is calculated. Let the take the example from previous post shown in the figure-

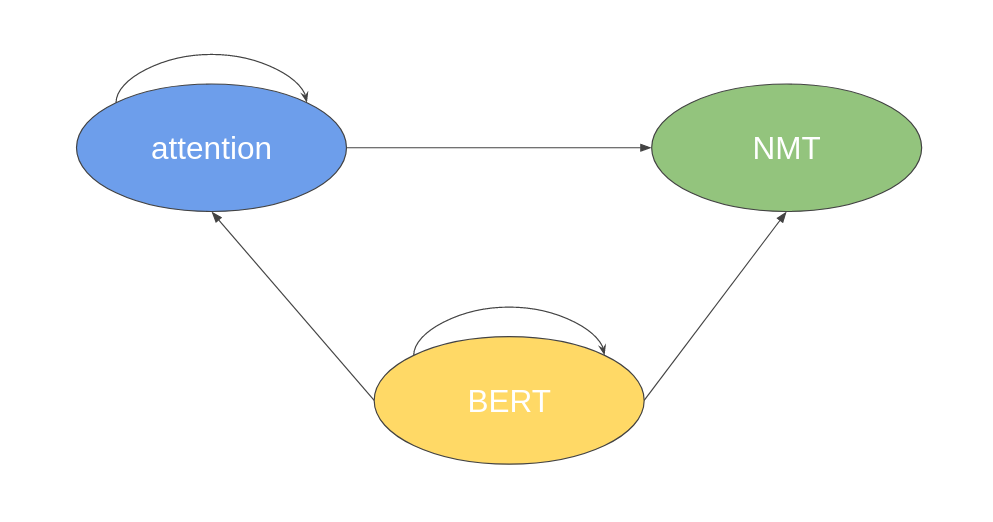
Fig1. Linked structure graph. We assign A to represent attention, B to represent BERT and N to represent NMT in the following example.

Before we calculate PageRank, as part of the preprocessing we need to remove all self-links and combine multiple links to the same node. Our new figure will look something like this:

Fig2. Graph after removing self-links. Note that there are no mulitple links in this example.

Then we use the following formula to calculate the PageRank of any node u:

$$ PR(u)= \frac{1-d}{N} + d (\Sigma \frac{PR(v)}{L(v)}) $$ where d is the damping factor(a value between 0.8 and 0.9), N is the total number of webpages, and v is the set of webpages that have a incoming link to u.

The main intuition is that PageRank is like water flowing through the network of nodes and links and getting accumulated at important nodes. Each node divides its water equally among the outgoing links. The extra factor 1-d/N represents the evaporation that allows the water to circulate among all the nodes othwerise it will get stuck at the important or sink nodes. The water at every node soon reaches the steady-state and this steady state value is called PageRank for that node.

Step 1: Assume, PageRank of all nodes to be 1 and the dampling factor d to be 0.80. It doesn't matter what value of PageRank you start with since the PageRank values converges to the same steady-state values. For a detailed explaination, see the reference number 2.

Correlation and Causation

September 26, 2020

It is such an interesting topic that I could not stop myself from writing a post. Every day, when I read newspapers or watch television, I see the following type of arguments:

• A tenant moves into an apartment. The owner meets with an accident and breaks his leg. He blames the tenant's arrival for the misfortune.
• A cat crossed the road while the woman was going to market. Something bad is going to happen to her or the family as the cat crossing one's path is a bad omen.
• Whenever I go to a particular temple, my wishes are always heard.
• If a black crow crows on top of your house, you are going to have a guest come over soon at your house. 
• Whenever Mr. X leaves his house and goes for a walk, it rains.
• One should not travel towards the east on Mondays and Saturdays. 
• Shaving on Saturdays can bring you bad luck. 

I could go on and on. I hope you got the idea. It sounds bewildering that a lot of people still believe in these kinds of ideas. I asked a few people their reason for belief and they said it's because their ancestors had believed in them and thus they believe too. A few said they had experienced it themselves and thus believe in it. 

The question is- Are these people right or wrong? Frederick Nietzsche, a great German philosopher would have said- nothing is right or wrong, it just depends upon the perspective. I would like to take a logical approach to this question. There are two things happening here- correlation and causation. Let's see what they mean.

Correlation means there is a relationship or pattern between the values of two variables. For e.g if the sales of ice-cream increase with the sales of ACs then there is a correlation (positive) between sales of ACs. Similary, if the sales of ice-cream increase when the sales of jackets decrease, then there is a correlation(negative) between sales of ice-cream and sales of jackets.

On the other hand, 

Causation means that one event causes another event to occur. For e.g the increase in sales of ice-cream and increase in sales of ACs happened due to an increase in temperature. Similary, the increase in sales of ice-cream and decrease in sales of jacket due to an increase in temperature. 

Thus, we can see that although these concepts seem very similar, they are very different. And the error in recognizing when one has happened but not the other, can lead to types of argument showed at the beginning of this post.

When we say that event A has happened and event B has happened either concurrently or one after the other, then we say that these two are random events and have just taken place. There may or may not be a relation between them. If an increase in quality or quantity of one event is marked with an increase in quality or quantity of another event then we say these are positively correlated or an increase in quality or quantity of one event is marked with a decrease in quality or quantity of another event then we say these are negatively correlated.  If there is no such increase or decrease then they are uncorrelated. An example of uncorrelated events could be sales of ice-cream and sales of cell-phones since one is independent of the other in general.

Now, in order to prove that one event has caused the other to happen then we need to show the causality. We need to show that there is a third factor that may be causing both variables to change else we attribute it to coincidence. And it turns out most of the time, for a causal relationship people have been able to find the actual causing factor. Let's take each example and see how can we prove or disprove the statements. 

•  "A tenant moves into an apartment. The owner meets with an accident and breaks his leg. He blames the tenant's arrival for the misfortune". These two are uncorrelated events. However, if the tenant kept something on the stairs which the owner couldn't see and tripped on it leading to the accident then this becomes a causal relationship. 
• "A cat crossed the road while the woman was going to market. Something bad is going to happen to her or the family as the cat crossing one's path is a bad omen". Again, the crossing of the road by the cat is not related to the ill-fortune of women unless the cat had some disease that could be transmitted to humans through the air like Coronavirus.
• "Whenever I go to a particular temple, my wishes are always heard."  Maybe you always go to the temple when you are confident of your actions or the situation seems to be favorable.
• "If a black crow crows on top of your house, you are going to have a guest come over soon at your house." This could happen if the crow watches the people coming to your house and only crows when it sees a familiar face. Or maybe your neighbor watches the crow and decides to pay you a visit if they liked the crow's voice. 
• "Whenever Mr. X leaves his house and goes for a walk, it rains." Mr. X lives in a house with no air-conditioning system and when the humidity becomes unbearable he decides to take a walk. High humidity makes the cloud precipitate. 
• "One should not travel towards the east on Mondays and Saturdays."  This one is beyond my ken. If you could think up of a reason then please let me know.
• "Shaving on Saturdays can bring you bad luck." You may be a working person who doesn't get time to shave during weekdays so that when you save on Saturdays you appear to be young and immature. Thus, people do not take you seriously during one or two days or you consider it to be your ill-fate.

 We can see that it requires us to dig deeper to search the actual cause. Most people, following Netwon's first law, tend to remain passive and follow whatever people have said in the past without actually questioning it. This leads to a society where superstitions and beliefs overshadow science and common-sense. Thus, it becomes necessary to question all such "confoundings" we see everyday around in our life.

Anything which is just a coincidence is of no practical use. Just imagine, if the people who made the airplanes (Wright bros) would have said- We see that whenever we attach wings to a plane, it flies. Now, if they would not have found out the actual mechanics of it, we could never have trusted a plane to fly with since planes without wings also fly (helicopters). Thus, if you believe in planes and fly in it, you should think about not leaving things to coincidence. 

PS: Interestingly, there is a name for these types of fallacies in Latin: cum hoc ergo propter hoc  and post hoc ergo propter hoc. Follow the links to know more about it.